The Newton-Raphson Algorithm

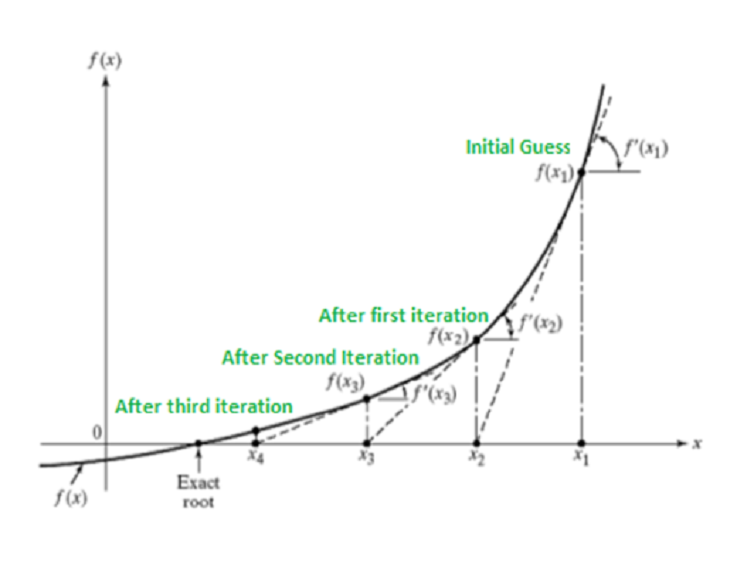
The Newton-Raphson Algorithm, also known as the Newton-Raphson Method or Newton's Method, is a powerful root-finding algorithm used to find the roots (or zeros) of a real-valued function. It is an iterative method that approximates the roots of a function by successively finding better approximations to the roots starting from an initial guess.

1. Root-finding algorithm: The Newton-Raphson Algorithm is a numerical method designed to find the roots (or zeros) of a function. A root of a function f(x) is a value of x for which f(x) = 0. Finding roots is a fundamental problem in mathematics and has numerous applications in various fields, such as engineering, physics, and computer science.
2. Real-valued function: The algorithm is specifically designed to find roots of real-valued functions, which means that the function takes real numbers as input and produces real numbers as output. It is not directly applicable to complex-valued functions or vector-valued functions.
3. Iterative method: The Newton-Raphson Algorithm is an iterative method, which means that it starts with an initial guess for the root and then generates a sequence of better approximations by repeatedly applying a specific formula. Each iteration produces a new approximation that is closer to the actual root than the previous approximation.
4. Successive approximations: The algorithm works by successively finding better approximations to the roots. It does not provide the exact root in a single step but rather converges towards the root as the iterations progress. The accuracy of the approximation improves with each iteration, provided that the initial guess is reasonably close to the actual root.
5. Initial guess: The algorithm requires an initial guess for the root, which is a starting point for the iterations. The choice of the initial guess can significantly impact the convergence rate and the number of iterations required to reach the desired accuracy. A good initial guess, which is close to the actual root, can lead to faster convergence, while a poor initial guess may result in slower convergence or even divergence (failure to converge).
6. Powerful algorithm: The Newton-Raphson Algorithm is considered a powerful root-finding algorithm because it typically converges rapidly, especially when the initial guess is close to the actual root. If the function and its derivative are well-behaved (continuous and differentiable) in the vicinity of the root, the algorithm can achieve quadratic convergence, meaning that the number of correct digits in the approximation approximately doubles with each iteration.

Newton-Raphson Algorithm is an iterative numerical method that starts with an initial guess and repeatedly refines the approximation to find the roots of a real-valued function. Its power lies in its ability to converge rapidly towards the root, provided that the initial guess is sufficiently close and the function satisfies certain conditions.

Basic Idea

The fundamental concept behind the Newton-Raphson Algorithm is to find the root of a function f(x) by finding the x-intercept of the tangent line to the function at a given point. The method starts with an initial guess for the root, x0, and iteratively updates the approximation by finding the x-intercept of the tangent line at the current approximation.

The iterative formula for the Newton-Raphson Algorithm is given by:

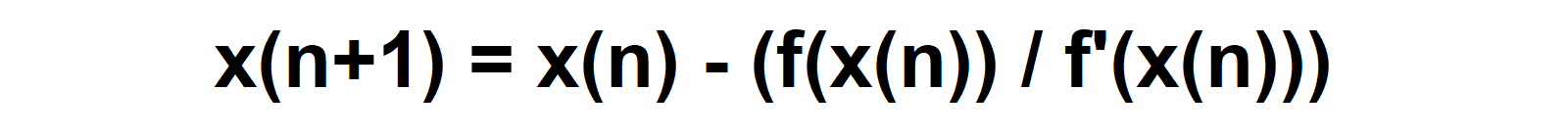
Where:

x(n+1) is the next approximation of the root.

x(n) is the current approximation of the root.

f(x(n)) is the value of the function at x(n).

f'(x(n)) is the value of the derivative of the function at x(n).

1. Root of a function: The goal of the Newton-Raphson Algorithm is to find the root (or zero) of a function f(x), which is the value of x for which f(x) = 0. Graphically, the root is the point where the curve of the function intersects the x-axis.
2. Tangent line approximation: The algorithm is based on the idea of approximating the function f(x) by its tangent line at a given point. The tangent line provides a linear approximation of the function in the vicinity of that point.
3. Initial guess: The algorithm starts with an initial guess, x0, for the root of the function. This initial guess can be obtained from prior knowledge, educated guesswork, or other suitable methods.
4. Tangent line at the initial guess: At the initial guess x0, the algorithm constructs the tangent line to the function f(x). This tangent line is a straight line that touches the curve of the function at the point (x0, f(x0)).
5. X-intercept of the tangent line: The x-intercept of the tangent line is the point where the tangent line crosses the x-axis. This x-intercept represents an improved approximation of the root, denoted as x1.
6. Iterative update: The algorithm then uses the x-intercept x1 as the new approximation for the root. It constructs a new tangent line at the point (x1, f(x1)) and finds the x-intercept of this new tangent line, which gives an even better approximation x2 for the root.
7. Successive iterations: This process of constructing tangent lines and finding their x-intercepts is repeated iteratively. Each iteration generates a new approximation xn+1 for the root, based on the tangent line at the previous approximation xn. In the iterative formula which is used for updating the approximation, f(x(n)) is the value of the function at the current approximation xn, and f'(x(n)) is the value of the derivative of the function at xn. This formula essentially finds the x-intercept of the tangent line at the point (xn, f(xn)).
8. Convergence: As the iterations progress, the approximations xn converge towards the actual root of the function, provided that the initial guess is sufficiently close to the root and the function satisfies certain conditions (e.g., continuity and differentiability).

The fundamental idea behind the Newton-Raphson Algorithm is to exploit the linear approximation provided by the tangent line to systematically improve the estimate of the root. By iteratively finding the x-intercepts of the tangent lines, the algorithm generates a sequence of approximations that converge towards the actual root of the function, starting from an initial guess.

Implementation

To implement the Newton-Raphson Algorithm, you need to follow these steps:

1. Choose an initial guess x0 for the root. The Newton-Raphson Algorithm requires an initial guess x0 as a starting point for the iterative process. This initial guess should be reasonably close to the actual root of the function for the algorithm to converge effectively. The choice of the initial guess can significantly impact the convergence rate and the number of iterations required to achieve the desired accuracy.

2. Calculate the value of the function f(x0) and its derivative f'(x0) at the initial guess. After selecting the initial guess x0, you need to evaluate the function f(x) at x0 to obtain f(x0). Additionally, you must calculate the value of the derivative of the function, f'(x), at x0 to obtain f'(x0). Both of these values are required in the iterative formula to compute the next approximation.

3. Use the iterative formula to calculate the next approximation x1. The iterative formula for the Newton-Raphson Algorithm is:

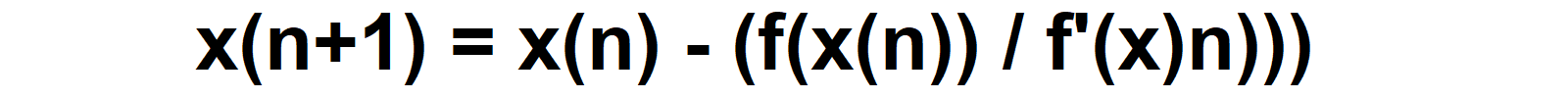
To calculate the next approximation x1, substitute x0 for x(n), f(x0) for f(x(n)), and f'(x0) for f'(x(n)) in the formula. This gives you the updated approximation x1, which should be closer to the actual root than the initial guess x0.

4. Repeat steps 2 and 3 until the desired accuracy is achieved or the maximum number of iterations is reached. The Newton-Raphson Algorithm is an iterative process, meaning that steps 2 and 3 need to be repeated multiple times. In step 2, you calculate the function value f(x1) and the derivative f'(x1) at the new approximation x1. Then, in step 3, you use these values to compute the next approximation x2 using the iterative formula.

This process continues, with each iteration generating a new approximation xn+1 based on the previous approximation xn, the function value f(xn), and the derivative f'(xn). The iterations are repeated until one of the following termination conditions is met:

1. The absolute difference between two successive approximations (|xn+1 - xn|) is less than a specified tolerance value (desired accuracy).
2. The absolute value of the function evaluated at the current approximation (|f(xn)|) is less than a specified tolerance value (desired accuracy).
3. The maximum number of iterations is reached (to prevent an infinite loop if the algorithm fails to converge).

The algorithm typically converges quadratically for initial guesses that are reasonably close to the root. This means that the number of correct digits approximately doubles with each iteration.

The implementation steps outline the process of selecting an initial guess, evaluating the function and its derivative at that guess, applying the iterative formula to compute the next approximation, and repeating this process until the desired accuracy is achieved or the maximum number of iterations is reached. The quadratic convergence behaviour ensures that the approximations quickly approach the actual root if the initial guess is sufficiently close.

Convergence and Termination

The Newton-Raphson Algorithm converges rapidly if the initial guess is sufficiently close to the root and if the function is well-behaved in the vicinity of the root. However, the algorithm may fail to converge or converge to a different root if the initial guess is too far from the desired root or if the function has multiple roots or inflection points.

To ensure convergence, the algorithm needs to satisfy certain conditions, such as:

1. The function should be continuously differentiable in the vicinity of the root.
2. The derivative of the function should not be zero at the root (i.e., f'(x) ≠ 0).

The termination criteria for the algorithm can be based on one or more of the following conditions:

1. The absolute difference between two successive approximations is less than a specified tolerance value.
2. The absolute value of the function evaluated at the current approximation is less than a specified tolerance value.
3. The maximum number of iterations is reached.

Convergence Conditions:

1. Initial guess sufficiently close to the root: The Newton-Raphson Algorithm relies on the initial guess being reasonably close to the actual root of the function. If the initial guess is too far away from the root, the algorithm may converge slowly or fail to converge altogether. The closer the initial guess is to the root, the faster the convergence rate will be.
2. Well-behaved function in the vicinity of the root: For the algorithm to converge effectively, the function should be well-behaved (continuous and differentiable) in the vicinity of the root. This means that the function should not have any discontinuities, sharp corners, or other irregularities near the root that could cause the algorithm to diverge or produce inaccurate results.
3. Failure to converge or convergence to a different root: If the initial guess is too far from the desired root, or if the function has multiple roots or inflection points (points where the derivative changes sign), the algorithm may fail to converge or converge to a root that is different from the desired one. This behavior can occur because the algorithm follows the path of the tangent line, which may lead it towards a different root or cause it to oscillate between multiple roots without converging.

Conditions for Convergence:

1. Continuous differentiability in the vicinity of the root: For the Newton-Raphson Algorithm to work correctly, the function must be continuously differentiable in the vicinity of the root. This means that both the function itself and its derivative must be continuous and have no discontinuities or sharp corners near the root. If this condition is not met, the algorithm may produce inaccurate results or fail to converge.
2. Non-zero derivative at the root: The derivative of the function should not be zero at the root, i.e., f'(x) ≠ 0. If the derivative is zero at the root, the algorithm will fail to converge because the tangent line at that point becomes horizontal, and the x-intercept of the tangent line (the next approximation) will be undefined.

Termination Criteria:

The Newton-Raphson Algorithm is an iterative process, and it needs a termination criterion to stop the iterations when a sufficiently accurate approximation of the root has been found or when convergence is unlikely. The termination criteria can be based on one or more of the following conditions:

1. Absolute difference between successive approximations: The algorithm can terminate when the absolute difference between two successive approximations (|xn+1 - xn|) is less than a specified tolerance value. This tolerance value represents the desired accuracy of the solution. If the difference between successive approximations is smaller than the tolerance, it implies that the algorithm has converged to a sufficiently accurate root.
2. Absolute value of the function at the current approximation: The algorithm can also terminate when the absolute value of the function evaluated at the current approximation (|f(xn)|) is less than a specified tolerance value. This condition checks if the current approximation is close enough to the true root, where the function value should be approximately zero.
3. Maximum number of iterations: To prevent an infinite loop in case the algorithm fails to converge or converges extremely slowly, a maximum number of iterations can be set as a termination criterion. If the algorithm reaches this maximum number of iterations without satisfying the other termination conditions, it will stop and report that convergence was not achieved.

These termination criteria ensure that the algorithm stops when a sufficiently accurate approximation of the root has been found or when further iterations are unlikely to improve the solution significantly. The choice of tolerance values and the maximum number of iterations depends on the specific problem and the desired accuracy of the solution.

Applications

The Newton-Raphson Algorithm is widely used in various fields, including:

1. Root-finding problems in mathematics and numerical analysis. One of the primary applications of the Newton-Raphson Algorithm is finding roots of mathematical functions in various areas of mathematics and numerical analysis. These include solving algebraic equations, transcendental equations, and finding zeros of complex functions.
2. Solving nonlinear equations in physics and engineering. Many physical systems and engineering problems involve nonlinear equations that need to be solved numerically. The Newton-Raphson Algorithm is widely used in fields such as mechanics, fluid dynamics, heat transfer, and electrical engineering to find solutions to these nonlinear equations.
3. Optimisation problems in machine learning and data analysis. In machine learning and data analysis, many optimization problems involve finding the roots or stationary points of objective functions or their derivatives. The Newton-Raphson Algorithm can be applied to these problems to find optimal solutions, such as minimizing a cost function or maximizing a likelihood function.
4. Computational finance and risk management. In finance and risk management, the Newton-Raphson Algorithm is used for various applications, such as option pricing, portfolio optimisation, and risk modelling. It is particularly useful for solving complex financial models that involve nonlinear equations or optimisations.

Despite its effectiveness, the Newton-Raphson Algorithm has some limitations, such as the requirement for the initial guess to be reasonably close to the root and the need for the function to be continuously differentiable.

Limitations:

1. Requirement for a good initial guess: The algorithm's convergence and performance heavily depend on the initial guess for the root. If the initial guess is not reasonably close to the actual root, the algorithm may converge slowly or fail to converge altogether. Choosing a good initial guess can be challenging, especially for complex functions or when little is known about the location of the roots.
2. Need for continuous differentiability: The Newton-Raphson Algorithm requires the function to be continuously differentiable in the vicinity of the root. If the function or its derivative is not continuous or differentiable at the root, the algorithm may fail to converge or produce inaccurate results.
3. Presence of multiple roots or inflection points: If the function has multiple roots or inflection points (points where the derivative changes sign), the algorithm may converge to a different root than the desired one, depending on the initial guess.
4. Computational complexity: While the Newton-Raphson Algorithm converges rapidly when the conditions are met, it requires computing the function and its derivative at each iteration, which can be computationally expensive for complex functions or high-dimensional problems.

In cases where these conditions are not met or when a good initial guess is unavailable, other root-finding methods, such as the Bisection Method or the Secant Method, may be more appropriate.

Alternative Methods:

1. Bisection Method: This method is suitable when the root is known to lie within a certain interval and does not require the computation of derivatives. However, it converges relatively slowly.
2. Secant Method: This method is similar to the Newton-Raphson Algorithm but does not require the computation of derivatives. It uses a secant line instead of a tangent line and can be useful when the derivative is difficult to compute or not available.
3. Fixed-Point Iteration: This method involves reformulating the equation as a fixed-point problem and iteratively applying a fixed-point function until convergence. It can be useful for certain types of equations but may suffer from slow convergence or non-convergence in some cases.

The choice of the root-finding method depends on the specific problem, the characteristics of the function, the availability of initial guesses, and the desired trade-off between convergence speed and computational complexity.